On MFAC and its Extensions

I.  On MFAC with literatur

Model Free Adaptive Control (MFAC) was initiated in Professor Hou’s seminal Ph.D. thesis in 1994, and thoroughly formalized in CRC Press book in 2013 and IEEE Trans. on Automatic Control regular paper in 2019. The systematic framework of MFAC theory is as follows

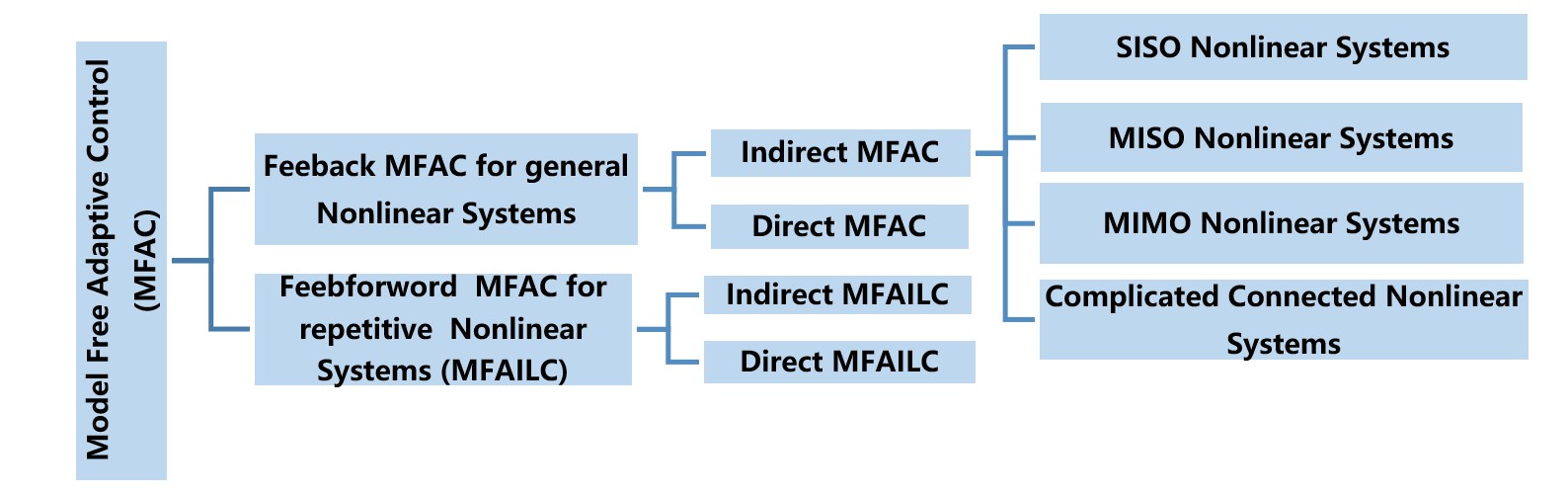
MFAC is a novel control theory with following characteristics: originality, integrity, correctness, superiority and applicability.

1.   Originality

Ø  Original basic concepts including, Pseudo Partial Derivative (PPD) or Pseudo Gradient (PG) for unknown SISO non-affine nonlinear system; Pseudo Jaccobian Matrix
 (PJM）or Partitioned Pseudo Jaccobian Matrix (PPJM）for unknown MIMO non-affine nonlinear system, as well as the coined term “Model Free Adaptive Control 
 (MFAC).”

Ø  Original basic mathematical tool for system and control theory: the equivalent dynamic linearization data modeling method, including the Compact Form Dynamic
  Linearization (CFDL),  the Partial Form Dynamic Linearization (PFDL), and the Full Form Dynamic Linearization (FFDL), data models for SISO/MISO/MIMO
   non-affine nonlinear systems

Ø  Original basic assumption for control system stability analysis: the generalized Lipschitz conditions for SISO/MISO/MIMO non-affine nonlinear systems, and the original 
 stability analysis approaches:the contraction mapping principle based stability analysis approaches rather than the overwhelming Lyapunov function methods for 
 SISO/MISO/MIMO non-affine nonlinear systems.

Ø  Original robustness concept and its analysis tool: the statistics-based influence analysises on the stability and tracking performance under the data-dropout, 
packet loss/disorder, or data noise, etc. for SISO/MISO/MIMO non-affine nonlinear systems.

2.      Integrity

Tab.1 Tab.1  Systematic framework of Indirect MFAC

Tab.Tab.2 Systematic framework of Direct MFAC

MFAC is a novel adaptive control method for unknown non-affine discrete-time nonlinear systems, which was initiated in 1994. The main feature of MFAC is that the control system design needs only the I/O data of the controlled process and does not include any information of the mathematical model. After about 30 years, it has been developed a systematic works. MFAC consists of indirect MFAC and direct MFAC, each kind of MFAC has following four dimensional framework, as follows: 1) Different controlled objects, including SISO/MISO/MIMO/complicated connected/ repetitive operation nonlinear systems; 2) Different dynamic linearization data models for a given nonlinear system, including the compact-form dynamic linearization (CFDL), partial-form dynamic linearization (PFDL), and full-form dynamic linearization(FFDL), data models; 3) Different parameter estimation algorithms for the parameters in the data model, including projection-type algorithms, least-square-type algorithms for the time-varying parameters, etc. 4) Different controller structure designing methods, such as optimal control, predictive control, learning control, etc.

Indirect MFAC has following matrix framework [1-2], shown as following Table 1. Different combination consists of different kinds of indirect MFAC schemes.

Direct MFAC, based on the dynamic linearization data model on the ideal controller for a given unknown nonaffine nonlinear system, is a novel MFAC, which transformed the control system designing problem explicitly into the identification issue of the designed linearized controller parameters, and it also has following matrix framework [3], shown as following Table 2. Different combination consists of different kinds of direct MFAC schemes.

3.      Correctness

The stability, monotonic convergence of the error dynamics, and internal stability of the MFAC schemes are proved rigorously. The stability analysis is based on the contraction mapping principle, not the Lyapunov stability theory. The contraction mapping based stability proof method is novel in the adaptive control research community, and it might be the fundamental method for control system design when the system model is unavailable.

The theoretical stability analysis for CFDL-MFAC scheme for SISO nonlinear systems is in [1，4], the PFDL-MFAC scheme is in [5], and most general FFDL-MFAC scheme is published in [6]. For MIMO cases, the stability results are in [7-8] for the different MFAC schemes.

4.      Superiority

MFAC has not only a systematic framework with rigorous stability guarantee, but also has progressiveness and compatibility with the other control methods.

   Ø  Since MFAC is designed by only using the measured closed-loop I/O data of the controlled plant, and the unsolvable theoretical problems in traditional model-based control theory, such as the accurate modeling and model reduction, the unmolded dynamics and robustness, the persistent excitation condition and the closed-loop control, etc., do not exist under the framework of MFAC theory owing to the fact that all the information of plant dynamics is included in the I/O measurement data.

  Ø  The well-known PID control and the traditional adaptive control for discrete-time linear time-invariant systems can be explicitly shown as the special cases of MFAC theoretically. Further, from the view point of MFAC, the traditional iterative learning control (ILC) theory for the discrete-time nonlinear systems can be regarded as the special case of MFAC in the iteration axis due to that the traditional ILC requires a pre-specified constructive controller structure and a constant control gain for the strictly repetitive task with ideal assumptions including the identical initial values, identical desired trajectory, and affine nonlinearity. The model free adaptive iterative learning control (MFAILC) consists of indirect MFAILC [9] and direct MFAILC [10-12]. All the controller forms in traditional ILC can be shown explicitly as special cases of MFAILC controllers, which is designed with a systematic theory-supported way in both indirect and direct MFAILC. Final, the learning errors for both kinds of MFAILC schemes are guaranteed to converge monotonically to zero in the normal distance measurement with rigorously mathematics analysis rather than the lambda norm sense.

  Ø  In additional, MFAC theory and the dynamic linearization data model methods have been used in many control theory branches to give birth to some novel data driven control methods or research directions, such as data driven model free multi-agent consensus or formation control, data driven sliding mode control, data driven networked control, data driven predictive control, event-triggered MFAC, data driven fault diagnosis and adaptive fault-tolerant control, data driven networked predictive control, observer based MFAC, MFAC under attacks, etc.
 

5.       Applicability

Until now, MFAC has been widely applied in many practical fields and the theoretical researches:

  Ø  MFAC has been recorded as at least with one whole chapter or section content in 14 monographs and 2 textbooks, including 4 English monographs, and one called Control Engineering Handbook. See Annex 1 for details.

  Ø  MFAC has been successfully applied in more than 230 different practical plants of different physical equipment, industrial field applications or the simulation examples with physical backgrounds. See Annex 2 for details.

  Ø  MFAC has been directly applied or studied with more than one chapter in 53 doctoral thesis, including 7 thesis from well-known foreign universities of USA, UK, Germany, Switzerland, Brazil, France, and Romania. Total 258 master dissertations focus on the MFAC improvements or applications. See Annex 2 for details.

  Ø  Till June of 2021, there are over 120 patents hold by others using MFAC theory as the key technology only within in China. See Annex 2 for details.

References

[1]      Z. S. Hou, The parameter identification, adaptive control and model free learning adaptive control for nonlinear systems, Ph.D. dissertation, Northeastern University, Shenyang, China, 1994.

[2]      Zhongsheng Hou and Shangtai Jin, “Model Free Adaptive Control: Theory and Applications,” CRC Press, Taylor & Francis Group, 2013

[3]      Zhongsheng Hou and Yuanming Zhu, Controller-Dynamic-Linearization Based Model Free Adaptive Control for Discrete-Time Nonlinear Systems, IEEE Transactions on Industrial Informatics, 9(4), 2013, pp2301-2309.

[4]      Z. S. Hou and W.H. Huang, The model-free learning adaptive control of a class of SISO nonlinear systems, American Control Conference, 1997, 343-344.

[5]      Z. S. Hou and S. T. Jin, A novel data-driven control approach for a class of discrete-time nonlinear systems, IEEE Transactions on Control Systems Technology, 2011, 19(6): 1549-1558.

[6]      Z. S. Hou, and S. S. Xiong, On Model-Free Adaptive Control and its Stability Analysis，IEEE Transactions on Automatic Control, 64(11), pp4555-4569, 2019

[7]      Z. S. Hou and S. T. Jin, Data-driven model-free adaptive control for a class of MIMO nonlinear discrete-time systems, IEEE Transactions on Neural Networks, 2011, 22(12): 2173-2188.

[8]      S. S. Xiong, Z. S. Hou, Model-Free Adaptive Control for Unknown MIMO Non-affine Nonlinear Discrete-time Systems with Experimental Validation，IEEE Transactions on Neural Networks and Learning Systems，DOI: 10.1109/TNNLS.2020.3043711

[9]      Ronghu Chi, and Zhongsheng Hou, Dual-stage optimal iterative learning control for nonlinear non-affine discrete-time systems, Acta Automatica Sinica, 33 (10), 1061-1065, 208

[10]   Z. S. Hou, X. Yu, and C. K. Yin, “A data-driven iterative learning control framework based on controller dynamic linearization,” in Proceedings of the 2018 Annual American Control Conference, Milwaukee, USA, 2018, pp. 5588–5593.

[11]   Xian Yu, Zhongsheng Hou, Marios Polycarpou, and Li Duan, Data-Driven Iterative Learning Control for Nonlinear Discrete-Time MIMO Systems, IEEE Transactions on Neural Networks and Learning Systems. DOI: 10.1109/TNNLS.2020.2980588

[12]   Xian Yu, Zhongsheng Hou, Marios Polycarpou, A Data-Driven ILC Framework for a Class of Nonlinear Discrete-Time Systems, IEEE Transactions on Cybernetics, DOI: 10.1109/TCYB.2020.3029596

II.  Data Driven Iterative Learning Control（DDILC）Theory and Applications

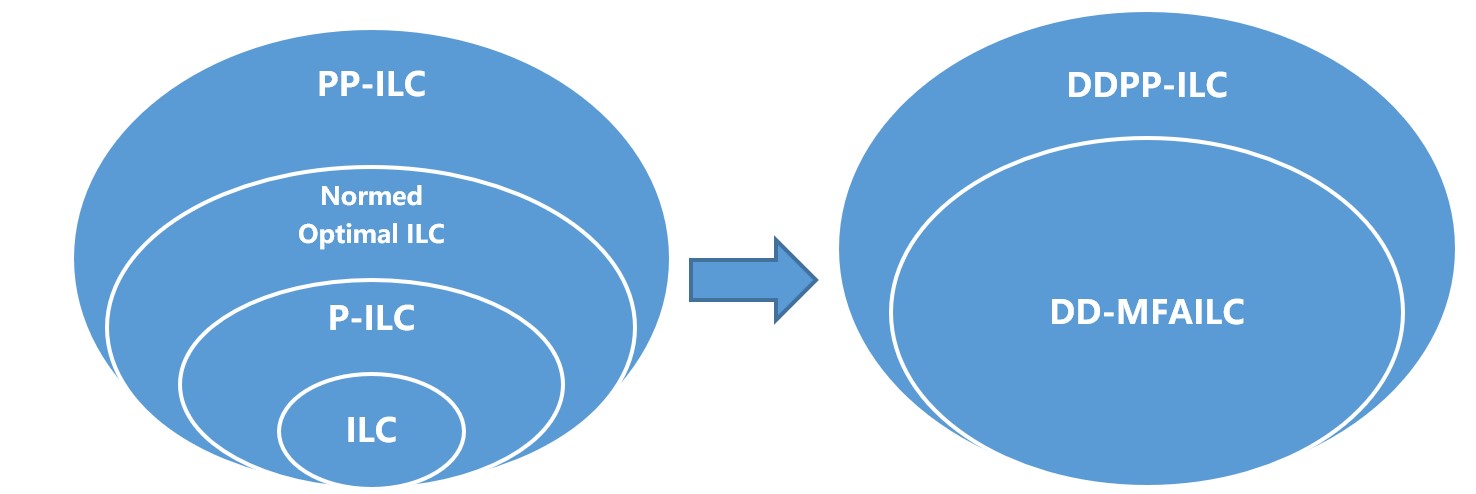
The conventional iterative learning control (ILC) could be classified into following three catalogs: Contraction mapping principle based ILC, composite energy functions based ILC, normed optimal ILC, and point-to-point ILC. Among them, only the contraction mapping principle based ILC method could be recognized as data driven control method since it controller structure is independent to the controlled plants but with a Lambda norm convergence analysis. The other three kinds of ILC are not a data driven control since their controller structure designs are depended on the model of the controlled plant, or their convergence analysis are heavily depended on the plant model structure. Besides, the following assumptions on the plant model are necessary for all the ILC methods abovementioned, that is, the identical initial values and the identical desired trajectory. The other common characteristics of the conventional ILC methods are that the learning controller structure is designed by an ad hoc way, and the controller gains are set to be constant.

The DDILC for unknown non-affine discrete-time nonlinear systems is a novel pure data-driven learning control method since all the components of the DDILC are designed in a systematic way with only the input/output data in the current and previous iterations. Further, DDILC is designed with guaranteed monotonic convergence in conventional 2-norm by using the dynamic linearization data modeling technique rather than the ad hoc way, and the optimization algorithms for controller’s structure determination and parameter tuning along the iteration axis. DDILC also includes indirect and direct DDILC[8-10]. DDILC has broken the fundamental limitations of traditional ILC which requires a constructive controller structure and a constant control gain for the strictly repetitive task with ideal assumptions including the identical initial values, identical desired trajectory, and affine nonlinearity. DDILC has re-shaped the prototype iterative learning control theory into data-driven paradigm. It paved a solid foundation for practical applications of ILC schemes. Further, the DDILC includes the most of the traditional ILC theory as a special case.

The most important point is that the DDILC methods are actually the extensions of MFAC theory on the iteration axis.

Literatures in DDILC

[1]      Xuhui Bu and Zhongsheng Hou, Iterative Learning Control Theory under the Networked Constraints, Science Press, 2019

[2]      Chi Ronghu, Zhongsheng Hou, Dual stage optimal iterative learning control for nonlinear non-affine discrete-time systems, Acta Automatica Sinica, 33(10), 1061-1065. 2007

[3]      Chenkun Yin, Jian-Xin Xu, Zhongsheng Hou, A High-order Internal Model Based Iterative Learning Control Scheme for Nonlinear Systems with Time-iteration-varying Parameters, IEEE Transactions on Automatic Control, 55(11), 2665-2670, 2010

[4]      Ronghu Chi, Zhongsheng Hou, Shangtai Jin, Danwei Wang and Jiangru Jian, Enhanced Data-driven Optimal Terminal ILC Using Current Iteration Control Knowledge, IEEE Transactions on Neural Networks and Learning Systems, 26(11), pp2939-2948, 2015

[5]      Ronghu Chi, Zhongsheng Hou, and Jianxin Xu, A discrete-time adaptive ILC for systems with iteration-varying trajectory and random initial condition, Automatica, 44,2207–2213, 2008.

[6]      Z. S. Hou, X. Yu, and C. K. Yin, A data-driven iterative learning control framework based on controller dynamic linearization, in Proceedings of the 2018 Annual American Control Conference, Milwaukee, USA, 2018, pp5588–5593.

[7]      Q Yu, Z Hou, X Bu, Q Yu, RBFNN-Based Data-Driven Predictive Iterative Learning Control for Nonaffine Nonlinear Systems, IEEE Transactions on Neural Networks and Learning Systems. 31(4), 1170-1182, 2020

[8]      X. Yu, Z. S. Hou and M. Polycarpou, A Data-Driven ILC Framework for a Class of Nonlinear Discrete-Time Systems, IEEE Trans. on Cybernetics, DOI: 10.1109/TCYB.2020.3029596

[9]      Xian Yu, Zhongsheng Hou, Marios Polycarpou, and Li Duan, Data-Driven Iterative Learning Control for Nonlinear Discrete-Time MIMO Systems, IEEE Transactions on Neural Networks and Learning Systems. DOI: 10.1109/TNNLS.2020.2980588

[10]   X Yu, Z Hou, MM Polycarpou, Distributed Data-Driven Iterative Learning Consensus Tracking for Nonlinear Discrete-Time Multi-Agent Systems, IEEE Transactions on Automatic Control, DOI 10.1109/TAC.2021.3105653

 DDILC theory has been successfully applied in traffic control fields, including road traffic signal control, freeway traffic control, and train operations control. The purpose of the applications is designed workable traffic control strategies by making fully utilization for the outstanding characteristics of the traffics, that is the repetitive operation pattern and the easily access to the big data of traffics in order to avoid the crucial time-consuming and inaccurate traffic modelling. See more details in https://assc.qdu.edu.cn/.

Traffic Control Applications of DDILC

[1]  Zhongsheng Hou and Jian-Xin Xu, Freeway traffic density control using iterative learning control approach, The IEEE 6th International Conference on Intelligent Transportation Systems, Shanghai, China, October 12-15, 2003

[2]  Zhongsheng Hou, Jian-Xin Xu and Hongwei Zhong, Freeway Traffic Control Using Iterative Learning Control Based Ramp Metering and Speed Signaling, IEEE Transactions on Vehicular Technology, 56(2), 466-477, 2007

[3]  Zhongsheng Hou and Ting Lei, Constrained Model Free Adaptive Predictive Perimeter Control and Route Guidance for Multi-Region Urban Traffic Systems, IEEE Transactions on Intelligent Transportation Systems, DOI: 10.1109/TITS.2020.3017351

[4]  Dai Li and Zhongsheng Hou, Perimeter Control of Urban Traffic Networks Based on Model-Free Adaptive Control, IEEE Trans.on Intelligent Transportation, 22(10), 2021, p6460-6472

[5]  Ye Ren, Zhongsheng Hou, Isik Ilber Sirmatel, and Nikolas Geroliminis, Data driven Model Free Adaptive Iterative Learning Perimeter Control for Large scale Urban Road networks, Transprotation Research, Part C. 115, 2020, 102618

[6]  Zhongsheng Hou and Yi Wang, Terminal Iterative Learning Control Based Station Stop Control of a Train, International Journal of Control, 84(7), 1263-1274, 2011

[7]  Heqing Sun, Zhongsheng Hou, and Dayou Li, Coordinated Iterative Learning Control Schemes for Train Trajectory Tracking with Overspeed Protection, IEEE Transactions on Automation Science and Engineering, 10(2), p323-333, 2013

[8]  Qiongxia Yu, Zhongsheng Hou and Jian-Xin Xu, D-type ILC based dynamic modeling and norm optimal ILC for high-speed trains, IEEE Transactions on Control Systems Technology, 26(2), pp652-663, 2018

[9]  Qiongxia Yu and Zhongsheng Hou, Adaptive Fuzzy Iterative Learning Control for High-Speed Trains with Both Randomly Varying Operation Lengths and System Constraints,  IEEE Transactions on Fuzzy Systems, 2021, 29(8):2408-2418.

[10]  Qian Wang , Shangtai Jin , and Zhongsheng Hou, Data-Driven Event-Triggered Cooperative Control for Multiple Subway Trains With Switching Topologies, IEEE Transactions on Intelligent Transportation Systems, Digital Object Identifier 10.1109/TITS.2021.3131997

III.  Data Driven Control

Professor Hou coined ‘data driven control (DDC)’ as a new branch of control theory in 2009[1]. Data-driven controls are the control theories and methods in which the controller is designed directly using on-line or off-line I/O data of the controlled system or knowledge from the data processing without using explicit or implicit information of the mathematical model of the controlled process, and whose stability, convergence, and robustness can be guaranteed by rigorous mathematical analysis under certain reasonable assumptions. In a short word, DDC designs control system directly only from the measured I/O data of the controlled plant, meanwhile to get out of all the inherent fundamental dilemmas in modern control theory, such as the unmodeled dynamics and robustness, the accurate modeling and model reduction, and the persistence of excitation condition and closed-loop control etc.

Due to his foresight and sagacity, he was invited to be a contributor on the report “Systems & Control for the future of humanity” by IFAC Task Road Map Committee[4]. DDC is now widely accepted in system and control community. The papers [1,2] are the first academic survey papers on the topic of DDC in the world, and they often be cited as the first literature in a journal paper on data driven control research.

[1]     Z. S. Hou, J.X. Xu, On data-driven control theory: the state of the art and perspective, Acta Automatica Sinica, 35 (6), 650-667, 2009.

[2]     Zhongsheng Hou and Zhuo Wang，From Model Based Control to Data Driven Control: Survey, Classification and Perspective, Information Sciences, 235(20), pp3-35, 2013.

[3]     Zhongsheng Hou, Ronghu Chi and Huijun Gao, An Overview of Dynamic-Linearization-Based Data-driven Control and Applications, IEEE Transactions on Industrial Electrnoics, vol. 64, no. 5, pp. 4076–4090, 2017.

[4]     Francoise Lamnabhi-Lagarrigue, Anuradha Annaswamy, Sebastian Engell, Alf Isaksson, Pramod Khargonekar, Richard M. Murray, Henk Nijmeijer, Tariq Samad, Dawn Tilbury, Paul Van den Hof, “Systems & Control for the future of humanity, research agenda: Current and future roles, impact and grand challenges,” Annual Reviews in Control, 43, pp1–64, 2017. Section 4.2.

[5]     Yongqiang Li and Zhongsheng Hou, Data-Driven Asymptotic Stabilization for Discrete-Time Nonlinear Systems, Systems &Control Letter, 64, 79-85, 2014

[6]     Yongqiang Li, Zhongsheng Hou, Yuanjing Feng and Ronghu Chi, Data-Driven Approximate Value Iteration with Analysis of Optimality Error Bound, Automatica, 78, p79-87, 2017